本文主要通过一个简单的 Demo 介绍 TensorFlow 初级 API 的使用方法,因为自己也是初学者,因此本文的目的主要是引导刚接触 TensorFlow 或者 机器学习的同学,能够从第一步开始学习 TensorFlow。阅读本文先确认具备以下基础技能:
TensorFlow 内部的计算都是基于张量的,因此我们有必要先对张量有个认识。张量是在我们熟悉的标量、向量之上定义的,详细的定义比较复杂,我们可以先简单的将它理解为一个多维数组:
3 # 这个 0 阶张量就是标量,shape=[]
[1., 2., 3.] # 这个 1 阶张量就是向量,shape=[3] [[1., 2., 3.], [4., 5., 6.]] # 这个 2 阶张量就是二维数组,shape=[2, 3] [[[1., 2., 3.]], [[7., 8., 9.]]] # 这个 3 阶张量就是三维数组,shape=[2, 1, 3]
TensorFlow 内部使用tf.Tensor类的实例来表示张量,每个 tf.Tensor有两个属性:
我们现在可以敲几行代码看一下 Tensor 。在命令终端输入 python 或者 python3 启动一个 Python 会话,然后输入下面的代码:
# 引入 tensorflow 模块 import tensorflow as tf # 创建一个整型常量,即 0 阶 Tensor t0 = tf.constant(3, dtype=tf.int32) # 创建一个浮点数的一维数组,即 1 阶 Tensor t1 = tf.constant([3., 4.1, 5.2], dtype=tf.float32) # 创建一个字符串的2x2数组,即 2 阶 Tensor t2 = tf.constant([['Apple', 'Orange'], ['Potato', 'Tomato']], dtype=tf.string) # 创建一个 2x3x1 数组,即 3 阶张量,数据类型默认为整型 t3 = tf.constant([[[5], [6], [7]], [[4], [3], [2]]]) # 打印上面创建的几个 Tensor print(t0)
print(t1)
print(t2)
print(t3)
上面代码的输出为,注意shape的类型:
>>> print(t0)
Tensor("Const:0", shape=(), dtype=int32) >>> print(t1)
Tensor("Const_1:0", shape=(3,), dtype=float32) >>> print(t2)
Tensor("Const_2:0", shape=(2, 2), dtype=string) >>> print(t3)
Tensor("Const_3:0", shape=(2, 3, 1), dtype=int32)
print 一个 Tensor 只能打印出它的属性定义,并不能打印出它的值,要想查看一个 Tensor 中的值还需要经过Session 运行一下:
>>> sess = tf.Session() >>> print(sess.run(t0)) 3 >>> print(sess.run(t1))
[ 3. 4.0999999 5.19999981] >>> print(sess.run(t2))
[[b'Apple' b'Orange']
[b'Potato' b'Tomato']] >>> print(sess.run(t3))
[[[5]
[6]
[7]]
[[4]
[3]
[2]]] >>> 数据流是一种常用的并行计算编程模型,数据流图是由节点(nodes)和线(edges)构成的有向图:
在 TensorFlow 中,每个节点都是用 tf.Tensor的实例来表示的,即每个节点的输入、输出都是Tensor,如下图中 Tensor 在 Graph 中的流动,形象的展示 TensorFlow 名字的由来
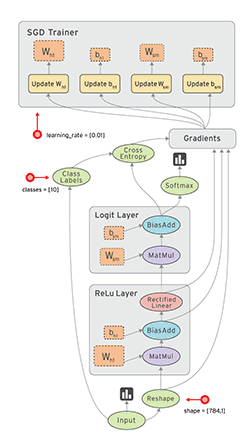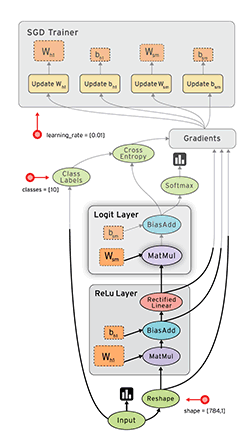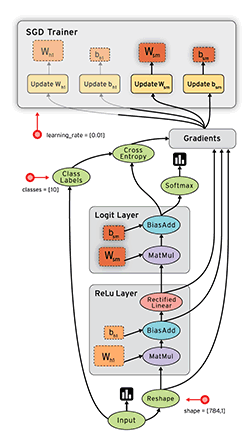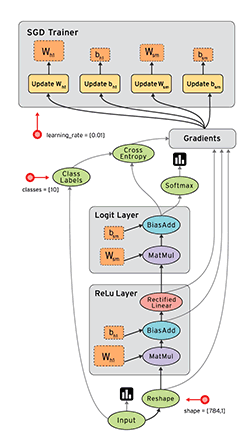
TensorFlow 中的数据流图有以下几个优点:
我们在Python中需要做一些计算操作时一般会使用NumPy,NumPy在做矩阵操作等复杂的计算的时候会使用其他语言(C/C++)来实现这些计算逻辑,来保证计算的高效性。但是频繁的在多个编程语言间切换也会有一定的耗时,如果只是单机操作这些耗时可能会忽略不计,但是如果在分布式并行计算中,计算操作可能分布在不同的CPU、GPU甚至不同的机器中,这些耗时可能会比较严重。
TensorFlow 底层是使用C++实现,这样可以保证计算效率,并使用 tf.Session类来连接客户端程序与C++运行时。上层的Python、Java等代码用来设计、定义模型,构建的Graph,最后通过tf.Session.run()方法传递给底层执行。
上面介绍的是 TensorFlow 和 Graph 的概念,下面介绍怎么用 Tensor 构建 Graph。
Tensor 即可以表示输入、输出的端点,还可以表示计算单元,如下的代码创建了对两个 Tensor 执行 + 操作的 Tensor:
import tensorflow as tf # 创建两个常量节点 node1 = tf.constant(3.2)
node2 = tf.constant(4.8) # 创建一个 adder 节点,对上面两个节点执行 + 操作 adder = node1 + node2 # 打印一下 adder 节点 print(adder) # 打印 adder 运行后的结果 sess = tf.Session()
print(sess.run(adder))
上面print的输出为:
Tensor("add:0", shape=(), dtype=float32) 8.0 上面使用tf.constant()创建的 Tensor 都是常量,一旦创建后其中的值就不能改变了。有时我们还会需要从外部输入数据,这时可以用tf.placeholder 创建占位 Tensor,占位 Tensor 的值可以在运行的时候输入。如下就是创建占位 Tensor 的例子:
import tensorflow as tf # 创建两个占位 Tensor 节点 a = tf.placeholder(tf.float32)
b = tf.placeholder(tf.float32) # 创建一个 adder 节点,对上面两个节点执行 + 操作 adder_node = a + b # 打印三个节点 print(a)
print(b)
print(adder) # 运行一下,后面的 dict 参数是为占位 Tensor 提供输入数据 sess = tf.Session()
print(sess.run(adder, {a: 3, b: 4.5}))
print(sess.run(adder, {a: [1, 3], b: [2, 4]}))
上面代码的输出为:
Tensor("Placeholder:0", dtype=float32) Tensor("Placeholder_1:0", dtype=float32) Tensor("add:0", dtype=float32) 7.5 [ 3. 7.] 我们还可以添加其他操作构建复杂的 Graph
# 添加×操作 add_and_triple = adder * 3. print(sess.run(add_and_triple, {a: 3, b: 4.5}))
上面的输出为
22.5
上面介绍了 TensorFlow 中的一些基本概念,下面我们通过一个小例子来了解一下怎么使用 TensorFlow 进行机器学习。
如下为我们进行某项实验获得的一些实验数据:
| 输入 | 输出 |
|---|---|
| 1 | 4.8 |
| 2 | 8.5 |
| 3 | 10.4 |
| 6 | 21 |
| 8 | 25.3 |
我们将这些数据放到一个二维图上可以看的更直观一些,如下,这些数据在图中表现为一些离散的点:
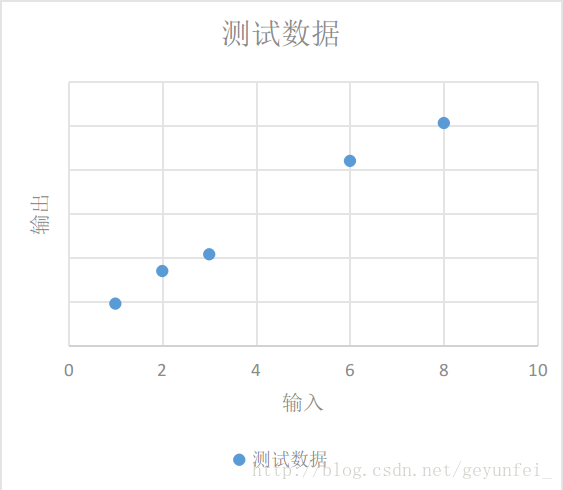
我们需要根据现有的这些数据归纳出一个通用模型,通过这个模型我们可以预测其他的输入值产生的输出值。
如下图,我们选择的模型既可以是红线表示的鬼都看不懂的曲线模型,也可以是蓝线表示的线性模型,在概率统计理论的分析中,这两种模型符合真实模型的概率是一样的。
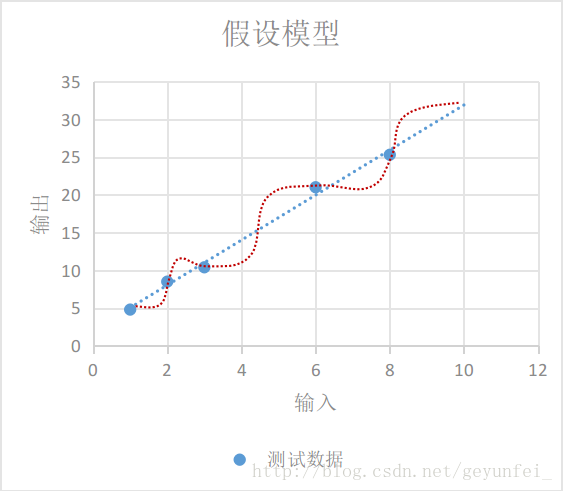
根据 “奥卡姆剃刀原则-若有多个假设与观察一致,则选最简单的那个,蓝线表示的线性模型更符合我们的直观预期。
如果用 xx 表示输入, yy 表示输出,线性模型可以用下面的方程表示:
如下图每条黄线代表线性模型计算出来的值与实际输出值之间的差值:
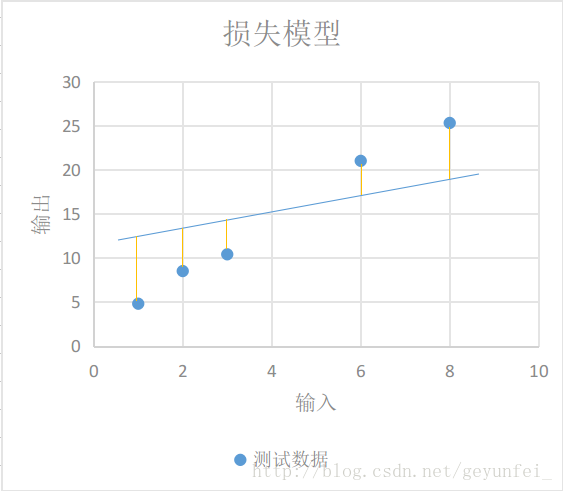
我们用y′y′表示实验得到的实际输出,用下面的方程表示我们的损失模型:
显然,损失模型里得到的lossloss越小,说明我们的线性模型越准确。
上面我们根据实验数据建立了一个线性模型,并为这个线性模型设计了一个损失模型,下面介绍的是怎么在 TensorFlow 中实现我们设计的模型。
在我们的线性模型 y=W×x+by=W×x+b 中,输入xx可以用占位 Tensor 表示,输出yy可以用线性模型的输出表示,我们需要不断的改变WW和bb的值,来找到一个使lossloss最小的值。这里WW和bb可以用变量 Tensor 表示。使用tf.Variable()可以创建一个变量 Tensor,如下就是我们模型的实现代码:
import tensorflow as tf # 创建变量 W 和 b 节点,并设置初始值 W = tf.Variable([.1], dtype=tf.float32)
b = tf.Variable([-.1], dtype=tf.float32) # 创建 x 节点,用来输入实验中的输入数据 x = tf.placeholder(tf.float32) # 创建线性模型 linear_model = W*x + b # 创建 y 节点,用来输入实验中得到的输出数据,用于损失模型计算 y = tf.placeholder(tf.float32) # 创建损失模型 loss = tf.reduce_sum(tf.square(linear_model - y)) # 创建 Session 用来计算模型 sess = tf.Session()
通过tf.Variable()创建变量 Tensor 时需要设置一个初始值,但这个初始值并不能立即使用,例如上面的代码中,我们使用print(sess.run(W))尝试打印W的值会得到下面提示未初始化的异常
tensorflow.python.framework.errors_impl.FailedPreconditionError: Attempting to use uninitialized value Variable 变量 Tensor 需要经过下面的 init 过程后才能使用:
# 初始化变量 init = tf.global_variables_initializer()
sess.run(init)
这之后再使用print(sess.run(W))打印就可以看到我们之前赋的初始值:
[ 0.1]
变量初始化完之后,我们可以先用上面对W和b设置的初始值0.1和-0.1运行一下我们的线性模型看看结果:
print(sess.run(linear_model, {x: [1, 2, 3, 6, 8]}))
输出结果为:
[ 0. 0.1 0.20000002 0.5 0.69999999]
貌似与我们实验的实际输出差距很大,我们再运行一下损失模型:
print(sess.run(loss, {x: [1, 2, 3, 6, 8], y: [4.8, 8.5, 10.4, 21.0, 25.3]}))
得到的损失值也很大
1223.05
我们可以用tf.assign()对W和b变量重新赋值再检验一下:
# 给 W 和 b 赋新值 fixW = tf.assign(W, [2.])
fixb = tf.assign(b, [1.]) # run 之后新值才会生效 sess.run([fixW, fixb]) # 重新验证损失值 print(sess.run(loss, {x: [1, 2, 3, 6, 8], y: [4.8, 8.5, 10.4, 21.0, 25.3]}))
输出的损失值比之前的小了很多:
159.94
我们需要不断调整变量W和b的值,找到使损失值最小的W和b。这肯定是一个very boring的过程,因此 TensorFlow 提供了训练模型的方法,自动帮我们进行这些繁琐的训练工作。
TensorFlow 提供了很多优化算法来帮助我们训练模型。最简单的优化算法是梯度下降(Gradient Descent)算法,它通过不断的改变模型中变量的值,来找到最小损失值。
如下的代码就是使用梯度下降优化算法帮助我们训练模型:
# 创建一个梯度下降优化器,学习率为0.001 optimizer = tf.train.GradientDescentOptimizer(0.001)
train = optimizer.minimize(loss) # 用两个数组保存训练数据 x_train = [1, 2, 3, 6, 8]
y_train = [4.8, 8.5, 10.4, 21.0, 25.3] # 训练10000次 for i in range(
上一个:Google 人工智能 TensorFlow 入门中文版
下一个:图像复原与重建
联系人:徐经理
手机:13907330718
电话:0731-22222718
邮箱:hniatcom@163.com
地址: 湖南省株洲市石峰区联诚路79号轨道智谷2号倒班房6楼603室